Planar Graphs Are Weird

Any simple planar graph can be drawn without crossings so that its edges are straight lines.

-Fáry’s Theorem

a graph $G$ is planar iff $G$ has no $K_5$-sub and no $K_{3, 3}$-sub

Kuratowski’s Theorem

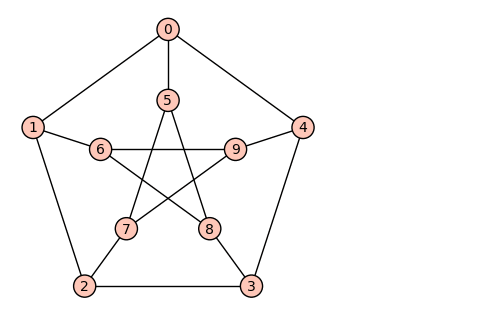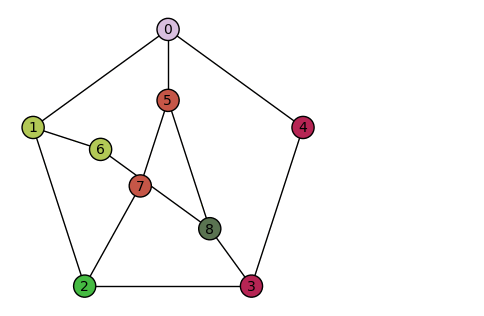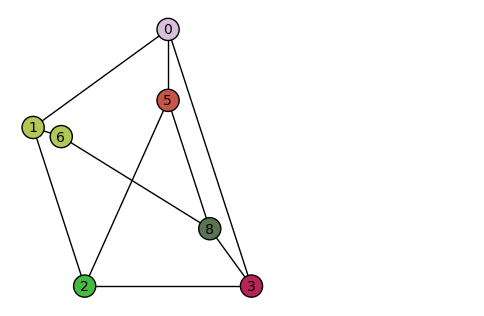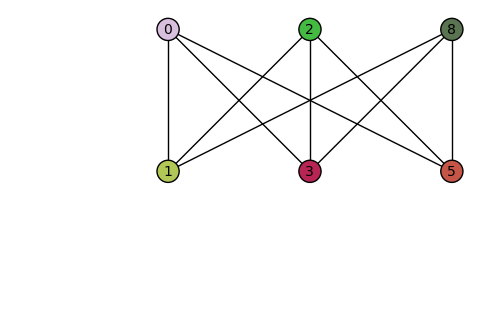
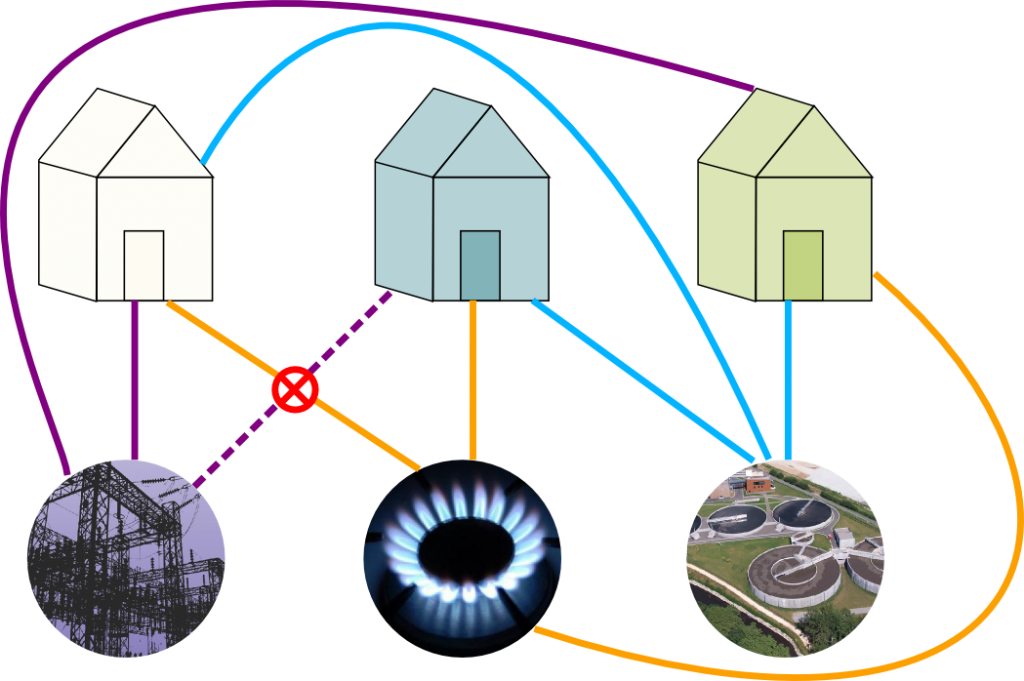
Have you ever heard of the 3 Utilities Problem?

You can color a planar graph with 4 colors so that adjacent color is not the same. The worst case is only in $K_4$. This is the upper bound.

If you have a map so that each country has different colors, you only need $4$ colors, this was conjectured by a cartographer, a map maker.

Let $G$ be a planar graph, $V$ and $E$ corresponds to the number of vertices and edges of $G$. $E \leq 3V - 6$ suffice.

$G$ is not planar and $G$ has no triangle, then $E \leq 2V - 4$

See that triangle is an odd cycle. Bipartite graph will always have no triangle.

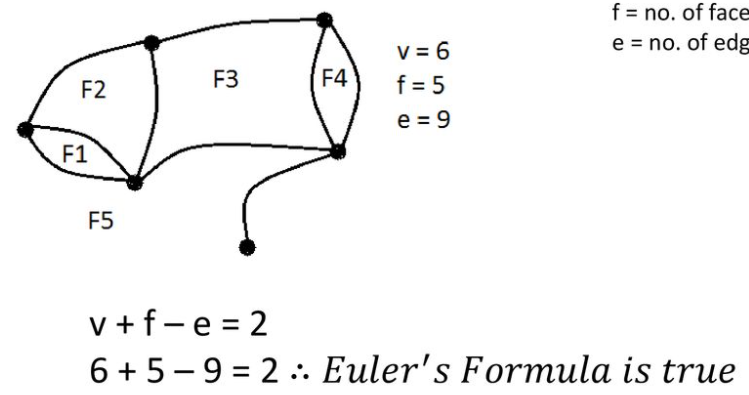
$V - E + F = 2$

References

• Medium - The Three Utilities Problem by Dhruv G.