Songwriter - Editorial

You are given the following problem: ICPC 2019 Jakarta E - Songwriter. My approach is a little bit different than the official solution, from my side, the tag is binary search, greedy, and a little bit of dynamic programming.

Let’s say the array given is $a$, of size $n$, indexed from $[0, n - 1]$ Lets iterate $i = [1, n)$. In each iteration, instead of storing the answer directly, instead we maintain an array of difference between each element.

For now, suppose $k = 2$, and ignore the $L$ and $R$, we only need to minimize the range between our answer.

Let’s check out the input in the following format

N K
a[0] a[1] a[2] ... a[N - 1]

Suppose you have the current input.

7 2
1 2 3 4 5 4 3

Define the answer array as $b$ indexed from $[0, n - 1]$. Now suppose we will start from $b[0] = 0$, when its going up, we must minimize the answer array lexicographically. Intuitively, we should not put to much of a difference, between $b[0]$ and $b[1]$, by that observation, we know that is when $a[i - 1] < a[i]$, then it’s true that $b[1] - b[0]$ at best be $1$. In general, when $a[i - 1] < a[i]$, then $b[i] - b[i - 1] = 1$. Let’s define the difference array as $c$, we can construct the $c$ instead of $b$. Because $c$ is just basically another basis representing $b$, with given starting value $b[0]$ and knowing $c$, we can construct the whole array $b$.

• Observation: At best, $c[i] = 1$ when $a[i -1] < a[i]$, at worst $c[i] = k$.

Let’s observe when it’s going down, to make it lexicographically minimum, we must set $c[i] = -k$. Meaning we must go as down as possible.

• Observation: At best, $c[i] = -k$ when $a[i - 1] > a[i]$, at worst $c[i] = -1$

• Observation: When $a[i - 1] = a[i]$, $c[i] = 0$.

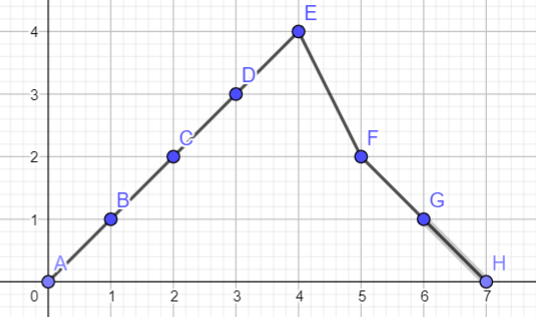
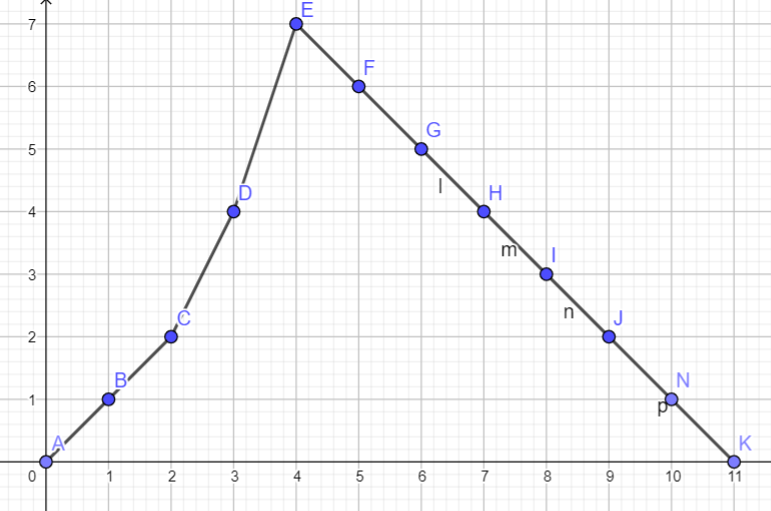
At first, I don’t define the array $c$, so it’s a little bit hard for me to imagine the solution. But check out this illustration.

In this illustration the array $c$ is

1 1 1 1 -2 -2

Observe that this is one of the best state for the given test cases. It’s true that we should do this, but what if the input is

8 2
1 2 3 4 5 4 3 2

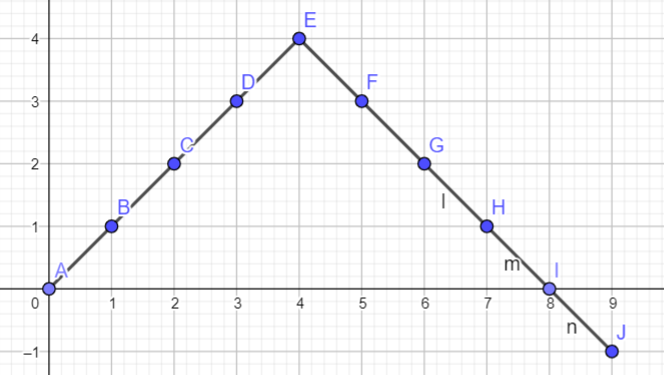
Can we still construct a solution following the previous solution? In fact, yes.

We can do this, check out that the array $c$ is now

1 1 1 1 -2 -1 -1

So we know that while the rightmost “Reducible” array can be made to fit a solution, it should be done.

Check out another test case, by then let’s ignore the array $a$’s constraints because we only need to know about its difference sign.

10 2
1 2 3 4 5 4 3 2 1 0

What to do with this? One, we can do this, and by this, it’s actually be equal to shifting the start in 1, while maintaining the lower bound of our $b$ non negative.

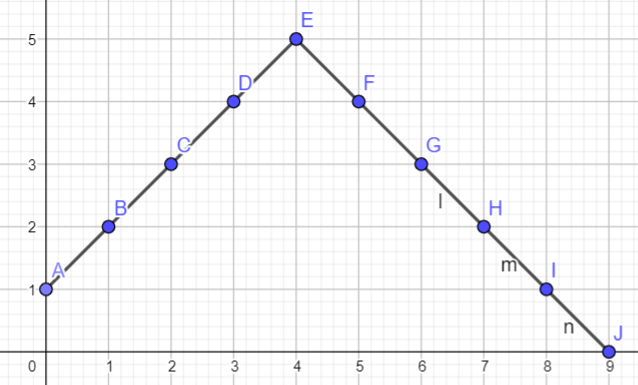
But, we do know, instead of moving it below the lower bound, let’s checkout all the “reducible” segments from $c$. before adding the last element. We know if $k = 2$, we can still extend $c[4]$ to $k$. This will increase the range, but still maintain the lexicographically minimum invariant.

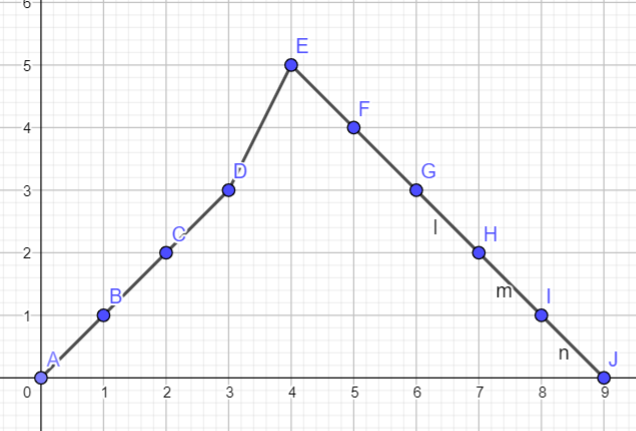
1 1 1 1 -1 -1 -1 -1

1 1 1 2 -1 -1 -1 -1 -1

If we want to add more negative value behind. When $k = 3$, we will allow this.

When $k = 2$ we will do this instead. Let’s see and observe that we will minimize going up (only moving by one), and maximizing going down, but still we have a lower limit of everything. Before we move on, let’s add another $-1$.

When $k = 3$, we may allow this

so yes, we should just maintain a stack of “reducible” $c$, and can greedily make it near $-1$, when $c[i] < 0$, and greedily make it near $k$, when $c[i] > 0$. In this way, we should be able to maintain the property. Now, what is the case, if all of them are full extended, meaning there are no more reducible $c$, it means, the starting node shouldn’t start at $0$ if we don’t want the $b$ goes below $0$.

Now, we should just binary search the starting point, that is whether to start at which node, because each reducible $c[i]$ is connected to each other, then we can assume that it’s safe to do it while the stack is not empty.

The invariant for the binary search is, we will minimize going up, maximize going down, maintaining all value $> 0$. If it can’t be done, than it means we shouldn’t start at the current $mid$.

Shown in the case

7 1
1 4 3 2

Which can’t start at $0$, if it start at $1$, the following can be achieved.

1 2 1 0

The invariant of the loop inside the binary search is, given a certain range, it’s possible for us not to exceed that length while fixing the lower bound and letting the upper bound free. The upper bound is set to free because it will always be minimized.

So the higher the $mid$ of binary search, basically increasing the range available, and fixing our lower bound meaning we will binary search the “range” (see that we’re going down maximally, meaning there won’t be any unnecessary space going up, we will greedily put the element as low as possible, but still $\geq 0$). And which if it can’t be done, it’s obvious that it cannot be done and we should increase our lower bound.

#include <bits/stdc++.h>
using namespace std;

#define fi first
#define se second
#define pb push_back
typedef long long LL;
typedef vector <LL> vi;
typedef pair<LL, LL> PII;
#define rep(i,a,b) for(int i = a;i < (b);i++)
#define trav(v, nx) for (auto &v : nx)
#define all(a) begin(a), end(a)
#define sz(a) (int) a.size()

int sign(LL n) {
  if (n == 0) return 0;
  return n / abs(n);
}

int main() {
  LL n, l , r, k;
  cin >> n >> l >> r >> k;
  vi isi(n);
  vi ans(n);
  for (auto &cur : isi) cin >> cur;
  // rep(i,1,n) cout << isi[i] << " " << isi[i - 1] << " " << sign(isi[i] - isi[i - 1]) << endl;
  LL kiri = 0;
  LL kanan = r - l + 5;
  while (kiri <= kanan) {
    LL mid = (kiri + kanan) >> 1;
    stack <LL> antri;
    LL cur = mid;
    ans.clear();
    bool can = 1;
    for (LL i = 1; i < n; i++) {
      if (isi[i - 1] < isi[i]) {
        ans.pb(1);
        cur++;
        antri.push(i - 1);
      } else if (isi[i - 1] == isi[i]) {
        ans.pb(0);
      } else {
        ans.pb(-k);
        cur -= k;
        antri.push(i - 1);
      }
      // cout << "Computing " << i << endl;
      // cout << cur << endl;
      while (cur < 0 && sz(antri)) {
        LL pos = antri.top();
        antri.pop();
        if (ans[pos] < 0) {
          LL curval = -ans[pos];
          LL butuh = min(curval - 1, -cur);
          cur -= ans[pos];
          ans[pos] += butuh;
          cur += ans[pos];
          if (ans[pos] < -1) antri.push(pos);
        } else {
          LL butuh = min(k - ans[pos], -cur);
          cur -= ans[pos];
          ans[pos] += butuh;
          cur += ans[pos];
          if (ans[pos] < k) antri.push(pos);
        }
      }
      if (cur < 0) {
        can = 0;
        break;
      }
    }
    if (kiri == kanan) break;
    if (can) kanan = mid;
    else kiri = mid + 1;
  }
  if (sz(ans) != n - 1) {
    cout << -1 << endl;
    return 0;
  }
  LL cur = l + kiri;
  vector <LL> jawab = {cur};
  if (cur > r || cur < l) {
    cout << -1 << endl;
    return 0;
  }
  for (LL i = 0; i < n - 1; i++) {
    cur += ans[i];
    assert(abs(jawab.back() - cur) <= k);
    // cout << sign(isi[i + 1] - isi[i]) << " " << sign(cur - jawab.back()) << endl;
    if (cur > r || cur < l || sign(isi[i + 1] - isi[i]) != sign(cur - jawab.back())) {
      cout << -1 << endl;
      return 0;
    }
    jawab.pb(cur);
  }
  assert(sz(jawab) == n);
  trav(cur, jawab) cout << cur << " ";
  cout << endl;
}